深度强化学习基础
该篇内容为学习 JoyRL Book 时所记录笔记,GitHub 项目地址:JoyRL-Book
# 绪论
# 强化学习相关概念
# 试错学习
试错学习(trial and error learning),即在不断地尝试和试错中学习到正确的策略。这个概念一开始是和行为心理学等工作联系在一起的,主要包括以下几个关键部分:
- 尝试:采取一系列动作或行为来尝试解决问题或实现目标。
- 错误:在尝试的过程中可能会出现错误,这些错误可能是环境的不确定性导致的,也可能是自身的不当行为导致的。
- 结果:每次尝试的后果,无论是积极的还是消极的,都会对下一次尝试产生影响。
- 学习:通过不断地尝试并出现错误,自身会逐渐积累经验,了解哪些动作或行为会产生有利的结果,从而在下一次尝试中做出更加明智的选择。
试错学习是强化学习中最鲜明的要素之一,但并不是强化学习的全部,强化学习还包含其它的学习形式例如观察学习(对应模仿学习、离线强化学习等技术)。
# 序列决策
在学习过程中个人做出的每一次尝试都是是一次决策(decision),每一次决策都会带来相应的结果,这个结果可能是即时的,也可能是延时的。我们把好的结果称为奖励(reward),坏的结果称为惩罚(punishment),或者负的奖励。最终通过一次次的决策来实现目标,这个目标通常是以最大化累积的奖励来呈现的,这个过程就是序列决策(sequential decision making)过程。
强化学习就是解决序列决策问题的有效方法之一。换句话说,对于任意问题,只要能够建模成序列决策问题或者带有鲜明的试错学习特征,就可以使用强化学习来解决,并且这是截至目前最为高效的方法之一。
# 强化学习方向概述
强化学习在游戏、机器人、金融等众多领域均有应用,其技术方向也很丰富。强化学习的典型应用有:多智能体强化学习、从数据中学习、探索策略、实时环境、多任务强化学习等等。
# 深度学习与强化学习
深度学习在强化学习中扮演的角色主要是提供了一个强大的函数拟合能力,使得智能体能够处理复杂、高维度和非线性的环境。
深度学习与强化学习之间的关系相当于眼睛和大脑的关系,眼睛是帮助大脑决策更好地观测世界的工具,对于一些没有眼睛的动物例如蚯蚓也可以通过其他的感官来观测并解析状态。再比如,同样大脑水平下,即相同的强化学习算法条件下,正常人要比双目失明的人日常的决策要更方便。但是,即使深度学习部分是相同的,例如正常大人和小孩都能通过眼睛观测世界,然由于大脑决策水平的差异也会让两者表现有所差异。
总而言之,深度与强化在更复杂的环境下缺一不可。最后,尽管强化学习算法很多,但基本上就分为两类,即基于价值的和基于策略梯度的算法,这两种算法各有优势,根据实际需要选择即可。
# 马尔可夫决策过程
马尔可夫决策过程是强化学习的基本问题模型之一,它能够以数学的形式来描述智能体在与环境交互的过程中学到一个目标的过程。这里智能体充当的是作出决策或动作,并且在交互过程中学习的角色,环境指的是智能体与之交互的一切外在事物,不包括智能体本身。状态指的是在执行动作时观测到的一些信息。
下图描述了马尔可夫决策过程中智能体与环境的交互过程。智能体每一时刻都会接收环境的状态,并执行动作,进而接收到环境反馈的奖励信号和下一时刻的状态。
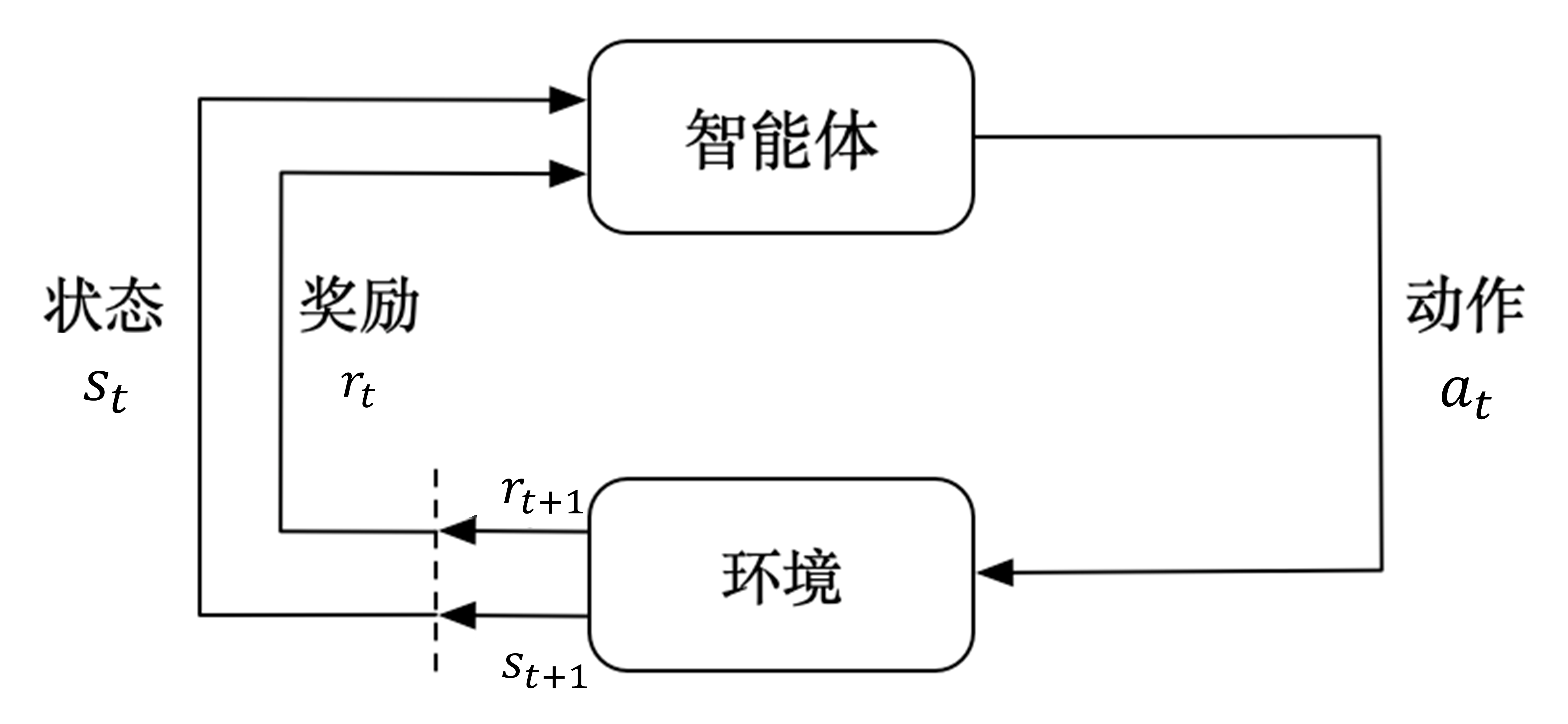
智能体与环境之间是在一系列离散的时步(time step)交互的,一般用 t 来表示,t=0,1,2,... (这里的 t=0 和 t=1 之间是跟现实时间无关的,取决于智能体每次交互并获得反馈所需要的时间)。在每个时 t , 智能体会观测或者接收到当前环境的状态 , 根据这个状态 执行动作 。执行完动作之后会收到一个奖励 , 同时环境也会收到动作的影响变成新的状态,并且在 t+1 时步被智能体观测到,如此循环得到交互过程轨迹如下:
此外,在强化学习中我们通常考虑的是有限马尔可夫决策过程(Finite MDP),即 t 是有限的,这个上限一般用 T 表示,也就是当前交互过程中的最后一个时步或最大步数,从 t=0 和 t+T 这一段时步我们称为一个回合(episode),比如游戏中的一局。
# 马尔可夫性质
马尔可夫决策过程的一个前提,即马尔可夫性质。
上式表示在已知所有之前的状态 的条件下,下一个状态 发生的概率与在已知当前状态 的条件下,下一个状态 发生的概率相等。
在给定历史状态 的情况下,某个状态的未来只与当前状态 有关,与历史的状态无关。
这个性质其实对于很多问题有着非常重要的指导意义的,因为这允许我们在没有考虑系统完整历史的情况下预测和控制其行为。实际问题中,有很多例子其实是不符合马尔可夫性质的,比如我们所熟知的棋类游戏,因为在我们决策的过程中不仅需要考虑到当前棋子的位置和对手的情况,还需要考虑历史走子的位置例如吃子等。但是在具体的情境下,当我们要解决问题不能严格满足马尔可夫性质的条件时,是可以结合其他的方法来辅助强化学习进行决策的。
# 回报
马尔可夫决策过程中智能体的目标是最大化累积的奖励,通常我们把这个累积的奖励称为回报(Return),用 表示,最简单的回报公式可写作:
其中 T 表示最后一个时步,也就是每回合的最大步数。这个公式其实只适用于有限步数的情境,例如玩一局游戏,无论输赢每回合总是会在有限的步数内会以一个特殊的状态结束,这样的状态称之为终止状态。但也有一些情况是没有终止状态的,换句话说智能体会持续与环境交互,比如人造卫星在发射出去后会一直在外太空作业直到报废或者被回收,这样的任务称之为持续性任务。在持续性任务中上述公式不适用,因为此时 。
为了解决这个问题,引入一个折扣因子(discount factor),并可以将回报表示为:
其中 取值范围在 0 到 1 之间,它表示了我们在考虑未来奖励时的重要程度,控制着当前奖励和未来奖励之间的权衡。换句话说,它体现了我们对长远目标的关注度。当 时,我们只会关心当前的奖励,而不会关心将来的任何奖励。而当 接近 1 时,我们会对所有未来奖励都给予较高的关注度。
这样做的好处是会让当前时步的回报 跟下一个时步的回报 是有所关联的,对于所有 t < T ,有下式:
# 状态转移矩阵
当前主要讨论有限状态马尔可夫决策过程(finite MDP),即状态的数量必须是有限的,无论是离散的还是连续的。如果状态数是无限的,此时通常会用另一种方式来对问题进行建模,称之为泊松(Poission)过程,又称为连续时间马尔可夫过程。然而在绝大部分强化学习实践场景中,泊松过程并不常见,对相关理论感兴趣可自行研究。
既然状态数有限,我们就可以用一种状态流向图的形式表示智能体与环境交互过程中的走向。举个例子,学生在上课时一般会有三种状态,认真听讲、玩手机和睡觉,分别用 和 表示。我们知道在马尔可夫决策过程中一般所有状态之间都是可以相互切换的,当学生在认真听讲时能切换到玩手机或者睡觉的状态,在睡觉时也可能继续睡觉,也可能醒过来认真听讲或者玩手机。如下图所示,图中每个曲线箭头表示指向自己,比如当学生在认真听讲即处于状态 时,会有 0.2 的概率继续认真听讲。当然也会分别有 0.4 和 0.4 的概率玩手机()或者睡觉()。此外,当学生处于状态 时,也会有 0.2 的概率会到认真听讲的状态(),像这种两个状态之间能互相切换的情况我们用一条没有箭头的线连接起来,参考无向图的表示。
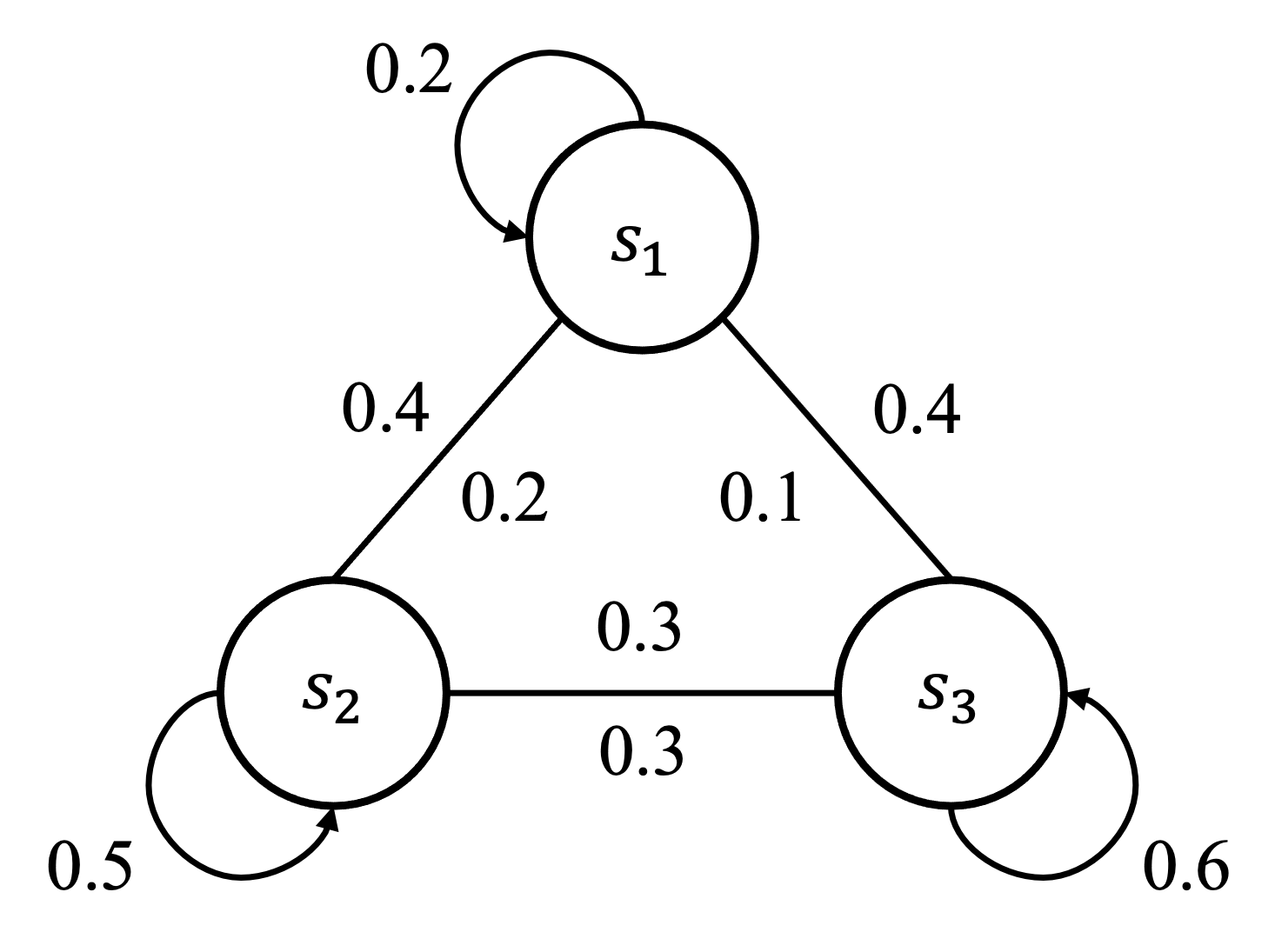
整张图表示了马尔可夫决策过程中的状态流向,这其实跟数字电路中有限状态机的概念是一样的。严格意义上来讲,这张图中并没有完整地描述出马尔可夫决策过程,因为没有包涵动作、奖励等元素,所以一般我们称之为马尔可夫链(Markov Chain),又叫做离散时间的马尔可夫过程(Markov Process),跟马尔可夫决策过程一样,都需要满足马尔可夫性质。因此我们可以用一个概率来表示状态之间的切换,比如
表示当前时步的状态 在下一个时步切换到 的概率,我们把这个概率称为状态转移概率(State Transition Probability)。拓展到所有状态我们可以表示为下式:
即当前状态是 s 时,下一个状态是 s' 的概率,其中大写的 S 表示所有状态的集合,即 = {, , } 。
由于状态数是有限的,将其概率绘制成表格如下:
| 0.2 | 0.4 | 0.4 | |
| 0.2 | 0.5 | 0.3 | |
| 0.1 | 0.3 | 0.6 |
在数学上也可以用矩阵来表示,如下:
这个矩阵就叫做状态转移矩阵(State Transition Matrix),拓展到所有状态可表示为:
其中 n 表示状态数,注意对于同一个状态所有状态转移概率加起来是等于 1 的,即 。
还有一个非常重要的点就是, 状态转移矩阵是环境的一部分 ,跟智能体是没什么关系的,而智能体会根据状态转移矩阵来做出决策。在这个例子中老师是智能体,学生的状态不管是认真听讲、玩手机还是睡觉这些老师是无法决定的,老师只能根据学生的状态做出决策,比如看见学生玩手机就提醒一下等等。
此外, 在马尔可夫链(马尔可夫过程)的基础上增加奖励元素就会形成马尔可夫奖励过程(Markov reward process, MRP) ,在马尔可夫奖励过程基础上增加动作的元素就会形成马尔可夫决策过程,也就是强化学习的基本问题模型之一。其中马尔可夫链和马尔可夫奖励过程在其他领域例如金融分析会用的比较多,强化学习则重在决策。
到这里我们就可以把马尔可夫决策过程描述成一个现今天常用的写法,即用一个五元组来表示 :
其中 S 表示状态空间,即所有状态的集合,A 表示动作空间,R 表示奖励函数,P 表示状态转移矩阵, 表示折扣因子。
# 动态规划
# 动态规划的编程思想
先看一道经点面试题:一个机器人位于一个 $ m\times n$ 网格的左上角 (起始点在下图中标记为 “S” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角即终点(在下图中标记为 “F” )。我们需要解决的问题是在这个过程中机器人可以有多少条不同的路径到达终点。
| S | * | * | * | * | * | * |
|---|---|---|---|---|---|---|
| * | * | * | * | * | * | * |
| * | * | * | * | * | * | F |
使用动态规划的做法,动态规划的解法主要有几个步骤:确定状态,写出状态转移方程和寻找边界条件。
在这个例题中我们首先可以定一个 ,表示从左上角即坐标为 到坐标 的路径数量,其中 以及 。由于机器人只能向右或者向下走,所以当机器人处于 的位置时,它的前一个坐标只能是上边一格 或者左边一格 ,这样一来就能建立出一个状态之间的关系,如式:
即走到当前位置 的路径数量等于走到前一个位置 和 的所有路径之和,这个就是状态转移方程。
此外我们需要考虑一些边界条件,因为在状态转移方程中 和 是不能等于 0 的,比如都等于 0 的时候会出现
,因此我们需要额外判断 和 等于 0 的情况。如下图 所示,首先考虑 的情况,即 ,显然此时机器人在起始点,从起始点到起始点 对应的路径数量必然是 1,对于 ,此时机器人会一直沿着网格左边沿往下走,这条路径上的所有 也都会是 1, 的情况同理。
| 1 (S) | 1 | 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 3 | 6 | 10 | 15 | 21 | 28 (F) |
因此状态转移方程可以完善为:
因此可以写出如下代码
def solve (m,n): | |
# 初始化边界条件 | |
f = [[1] * n] + [[1] + [0] * (n - 1) for _ in range (m - 1)] | |
# 状态转移 | |
for i in range (1, m): | |
for j in range (1, n): | |
f [i][j] = f [i - 1][j] + f [i][j - 1] | |
return f [m - 1][n - 1] |
一般 动态规划问题有三个性质,最优化原理、无后效性和有重叠子问题 。其中有重叠子问题不是动态规划问题的必要条件。无后效性指的是即某阶段状态一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只与当前状态有关,这其实就是前面所说的马尔可夫性质。而最优化原理是指,如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优化原理。马尔可夫决策过程的目标是最大化累积回报,根据回报公式,要解决 的问题,可以一次拆分成解决 $G_t,G_{t-1}, \cdots,G_1 $ 的问题,这其实就满足动态规划性质中的最优化原理。综合以上两点,我们可以利用动态规划的思想来解决强化学习问题,具体解决方法参考后面讲解的价值迭代和策略迭代算法。
# 状态价值函数和动作价值函数
在马尔可夫决策过程中,每个状态是有一定的价值的,可以定义为:
这就是状态价值函数(state-value function),从特定状态出发,按照某种策略 进行决策所能得到的回报期望值,注意这里的回报是带有折扣因子 的。
另外引入动作的元素后会有一个 函数,也叫做 动作价值函数(action-value function),即
由于我们遵循策略 来选择动作,我们可以将 表达为采取所有可能动作的期望回报的加权平均,其中每个动作的权重是该动作在给定状态下根据策略 被选择的概率
将动作价值函数代入得到
其中 表示策略函数,一般指在状态
下执行动作 的概率分布。公式表示在给定状态 的情况下,智能体所有动作的价值期望(所有动作价值函数乘以对应动作的概率之和)就等于该状态的价值,这其实就是利用了数学中的全期望公式。
# 贝尔曼方程
类比于回报公式 ,也可以对状态价值函数和动作价值函数做一个类似的推导,如下:
根据马尔可夫性质,未来回报依赖于下一个状态 而不是历史状态,因此可以将期望回报分解为立即回报和从下一个状态开始的期望回报的折现
立即回报 是在状态 下采取某个动作后立即获取的回报,它可以通过策略 和状态转移概率 来计算。由于我们考虑的是状态价值函数,不关心采取的具体动作,因此我们可以将立即回报写为状态 的函数
其中 是从状态 采取动作 到达状态 时获得的立即回报。
对于第二项,我们需要考虑从状态 转移到所有可能状态 的概率,并计算在这些状态下的价值函数的期望值。由于我们遵循策略 ,我们可以将 写为 的加权平均,权重是转移到每个状态的概率:
这里的 是从状态 转移到状态 的概率,它可以通过策略 和状态转移概率 来计算
将上述两部分的期望回报代入原始的期望回报表达式中,得到状态价值函数的贝尔曼方程
类似的,动作价值函数贝尔曼方程推导为:
在最优策略 下,状态价值函数也是最优的,相应的动作价值函数也最优。我们的目标是使得累积的回报最大化,那么最优策略下的状态价值函数可以表示为:
这个公式叫做贝尔曼最优方程(Bellman optimality equation), 对于动作价值函数也是同理
# 策略迭代
在最优策略下,对应的状态和动作价值函数也都是最优的。但是实际求解中在优化策略的过程中,同时我们还需要优化状态和动作价值函数,这其实是一个多目标优化的问题。
策略迭代算法的思路是分成两个步骤,首先固定策略 不变,然后估计对应的状态价值函数 ,这一叫做策略估计(policy evaluation)。然后根据估计好的状态价值函数
结合策略推算出动作价值函数 ,并对 函数优化然后进一步改进策略,这一步叫策略改进(policy improvement)。在策略改进的过程中一般是通过贪心策略来优化的,即定义策略函数为:
策略迭代算法的伪代码如下
初始化策略 π | |
重复直到收敛: | |
1. 策略评估(Policy Evaluation): | |
对于所有状态 s: | |
V (s) <- R (s, π(s)) + γ ∑ p (s'|s,π(s)) V (s') | |
直到 V (s) 的变化小于某个阈值 | |
2. 策略改进(Policy Improvement): | |
对于所有状态 s: | |
Q (s, a) <- R (s, a) + γ ∑ p (s'|s, a) V (s') | |
对于所有状态 s: | |
π(s) <- argmax_a Q (s, a) |
# 价值迭代
价值迭代算法相对于策略迭代更加直接,它直接根据以下公式来迭代更新。
价值迭代首先将所有的状态价值初始化,然后不停地对每个状态迭代,直到收敛到最优价值 ,并且根据最优价值推算出最优策略 。
价值迭代算法伪代码如下
初始化 V (s) 对于所有状态 s | |
重复直到收敛: | |
对于所有状态 s: | |
Q (s, a) <- R (s, a) + γ ∑ p (s'|s, a) V (s') | |
V (s) <- max_a Q (s, a) | |
直到 V (s) 的变化小于某个阈值 | |
对于所有状态 s: | |
π(s) <- argmax_a Q (s, a) |
这种情况下,其实比策略迭代算法要慢得多,尽管两种方法都需要多次遍历。但是在策略迭代算法中考虑了中间每个时步可能遇到的最优策略并及时加以改进,这意味着就算策略在早期并不完美(也许需要改进),策略迭代仍能够更快地接近最优解。

# 免模型预测
# 有模型与免模型
在前面的章节中,均默认了状态转移概率是已知的,这种情况下的算法称为有模型算法,但是对于大部分情况下的智能体,环境是未知的,这种情况下的算法称为免模型算法。
有模型的强化学习尝试先学习一个环境模型,它可以是环境的动态(例如,给定一个状态和一个动作,预测下一个状态)或奖励(给定一个状态和一个动作,预测奖励)。一旦有了这个环境模型,智能体可以使用它来计划最佳的行动策略,例如通过模拟可能的未来状态来预测哪个动作会导致最大的累积奖励。它的优点很明显,即可以在不与真实环境交互的情况下进行学习,因此可以节省实验的成本。但缺点是,这种模型往往是不完美的,或者是复杂到难以学习和计算。
免模型直接学习在特定状态下执行特定动作的价值或优化策略。它直接从与环境的交互中学习,不需要建立任何预测环境动态的模型。其优点是不需要学习可能是较为复杂的环境模型,更加简单直接,但是缺点是在学习过程中需要与真实环境进行大量的交互。注意,除了动态规划之外,基础的强化学习算法都是免模型的。
# 预测与控制
前面提到很多经典的强化学习算法都是免模型的,换句话说在这种情况下环境的状态转移概率是未知的,这种情况下会去近似环境的状态价值函数,这其实跟状态转移概率是等价的,我们把这个过程称为预测。换句话说,预测的主要目的是估计或计算环境中的某种期望值,比如状态价值函数 或动作价值函数 。例如,我们正在玩一个游戏,并想知道如果按照某种策略玩游戏,我们的预期得分会是多少。
而控制的目标则是找到一个最优策略,该策略可以最大化期望的回报。换句话说,你不仅想知道按照某种策略你的预期得分是多少,还想知道如何选择动作以最大化这个得分。控制问题通常涉及两个相互交替的步骤:策略评估(使用当前策略估计值函数)和策略改进(基于当前的值函数更新策略)。
在实际应用中,预测和控制问题经常交织在一起。例如,在使用 Q-learning(一种免模型的控制算法)时,我们同时进行预测 (更新 值) 和控制 (基于 值选择动作)。很多时候我们不能一蹴而就解决好控制问题,而需要先解决预测问题,进而解决控制问题。
# 蒙特卡洛估计
蒙特卡洛估计方法在强化学习中是免模型预测价值函数的方式之一,本质是一种统计模拟方法。
假设需要计算一个不规则图形的面积,这种情况下是很难通过规则或者积分的方式得到结果的。蒙特卡洛基于这样的想法:使用计算机程序生成大量均匀分布坐标点,让所有坐标点组成的范围能够完全覆盖不规则图形。然后统计出图形内的点数,通过它们占总点数的比例和坐标点生成范围的面积就可以求出图形面积。
假设上一章节的机器人在 需要寻找最短路径。我们用机器人的位置表示不同状态,即 ,机器人只能向下或者向右走,对应动作 $a_1 $ 和 $ a_2$ ,起点坐标 ,即初始状态 ,设定机器人每走一步接收到奖励为 ,折扣因子 。
使用蒙特卡洛方法,采样大量的轨迹,对于每个轨迹计算对应状态的回报然后取平均近似,称之为经验平均回报(empirical mean return)。根据大数定律,只要采样的轨迹数量足够多,计算出的经验平均回报就能趋近于实际的状态价值函数。当然,蒙特卡洛方法有一定的局限性,即只适用于有终止状态的马尔可夫决策过程。
蒙特卡洛方法主要分成两种算法,一种是首次访问蒙特卡洛(first-visit Monte Carlo,FVMC)方法,另外一种是每次访问蒙特卡洛(every-visit Monte Carlo,EVMC)方法。FVMC 方法主要包含两个步骤,首先是产生一个回合的完整轨迹,然后遍历轨迹计算每个状态的回报。注意,只在第一次遍历到某个状态时会记录并计算对应的回报。而在 EVMC 方法中不会忽略统一状态的多个回报。
使用 FVMC 估算某个马尔可夫决策过程(MDP)状态值函数的伪代码:
初始化: | |
对于所有状态 s,V (s) = 0 | |
N (s) = 0,对于所有状态 s | |
策略 π 用于选择动作 | |
G = 0 | |
对于每个 episode(序列): | |
初始化 S,为当前状态 | |
终止 = False | |
生成一个序列,直到达到终止状态: | |
选择动作 A 根据策略 π | |
执行动作 A,获得奖励 R 和下一个状态 S' | |
S = S' | |
如果是终止状态,则终止 = True | |
G = G + R | |
如果 S' 是第一次访问: | |
N (S') = N (S') + 1 | |
V (S') = V (S') + (G - V (S')) | |
直到 终止 |
使用 EVMC 估算某个马尔可夫决策过程(MDP)状态值函数的伪代码:
初始化: | |
对于所有状态 s,V (s) = 0 | |
N (s) = 0,对于所有状态 s | |
策略 π 用于选择动作 | |
G = 0 | |
对于每个 episode(序列): | |
初始化 S,为当前状态 | |
终止 = False | |
生成一个序列,直到达到终止状态: | |
选择动作 A 根据策略 π | |
执行动作 A,获得奖励 R 和下一个状态 S' | |
S = S' | |
如果是终止状态,则终止 = True | |
G = G + R | |
N (S) = N (S) + 1 | |
V (S) = V (S) + (G - V (S)) | |
直到 终止 |
FVMC 是一种基于回合的增量式方法,具有无偏性和收敛快的优点,但是在状态空间较大的情况下,依然需要训练很多个回合才能达到稳定的结果。而 EVMC 则是更为精确的预测方法,但是计算的成本相对也更高。
# 时序差分估计
时序差分估计方法是一种基于经验的动态规划方法,它结合了蒙特卡洛和动态规划的思想。最简单的时序差分可以表示为:
这种算法一般称为单步时序差分 (one-step TD),即 。可以看到,在这个更新过程中使用了当前奖励和后继状态的估计,这是类似于蒙特卡罗方法的;但同时也利用了贝尔曼方程的思想,将下一状态的值函数作为现有状态值函数的一部分估计来更新现有状态的值函数。此外,时序差分还结合了自举(bootstrap)的思想,即未来状态的价值是通过现有的估计 (也叫做时序差分目标)进行计算的,即使用一个状态的估计值来更新该状态的估计值,没有再利用后续状态信息的计算方法。这种方法的好处在于可以将问题分解成只涉及一步的预测,从而简化计算。此外,$ \delta = r_{t+1} + \gamma V (s_{t+1}) - V (s_t)$
被定义为时序差分误差(TD error)。
但有一点需要注意的是,由于基于时步的学习方式,并且终止状态没有下一步,比如当 是终止状态时, 是没有意义的。因此时序差分方法在实践过程中会把终止状态单独做一个判断,即将对应未来状态的估计值设置为 ,然后更新当前状态的估计值,这个过程也被称作回溯,如下式所示,后面所有基于时序差分的方法都会有这样的一个判断。
# 时序差分和蒙特卡洛的比较
时序差分方法和蒙特卡洛方法之间的差异如下图
- 时序差分方法可以在线学习(online learning),每走一步就可以更新,效率高。蒙特卡洛方法必须等游戏结束时才可以学习。
- 时序差分方法可以从不完整序列上进行学习。蒙特卡洛方法只能从完整的序列上进行学习。
- 时序差分方法可以在连续的环境下(没有终止)进行学习。蒙特卡洛方法只能在有终止的情况下学习。
- 时序差分方法利用了马尔可夫性质,在马尔可夫环境下有更高的学习效率。蒙特卡洛方法没有假设环境具有马尔可夫性质,利用采样的价值来估计某个状态的价值,在不是马尔可夫的环境下更加有效。

# n 步时序差分
把时序差分方法进一步拓展,之前只是向前自举了一步,即 ,我们可以调整为两步,利用两步得到的回报来更新状态的价值,调整 步就是 步时序差分 (n-step TD),如下式
我们会发现当 趋近于无穷大时,就变成了蒙特卡洛方法,因此可以通过调整自举的步数,来实现蒙特卡洛方法和时序差分方法之间的权衡。这个 我们通常会用 来表示,即 方法。
以下是一些常见的方法来选择合适的
- 网格搜索 (Grid Search):对于给定的一组 值,可以通过网格搜索方法在这些值中进行遍历,并评估每个值对应的算法性能。选择在验证集上表现最好的 值作为最终的选择。
- 随机搜索 (Random Search):随机选择一组 值,在验证集上评估每个值对应的算法性能。通过多次随机搜索,可以得到更好 值。
- 自适应选择:在训练过程中逐渐适应地调整 的取值。例如,可以在训练的早期使用较小的 值,以更多地依赖单步 TD 误差来减小偏差;在训练的后期逐渐增大 值,以更多地依赖多步回报来减小方差。
- 交叉验证 (Cross-validation):将数据集划分为多个子集,交叉验证不同的 值,并平均它们的性能评估结果。这样可以更好地估计不同 值的泛化性能。
- 经验取值:在某些情况下,根据先前的经验或已知的任务特性,可以选择一些常用的 取值作为初始值,并进一步微调。
需要注意的是,无论使用哪种方法, 的最佳取值可能因任务、环境和算法的不同而异。因此,选择合适的 值是一个实验过程,需要根据具体问题进行调整。在实际应用中,可以结合多种方法来找到最佳的 值,以获得更好的性能。
# 免模型控制
# Q-learning 算法
在前章节中我们知道,动作价值函数体现了策略与状态价值函数之间的联系。 因此,为了解决控制问题,我们只需要直接预测动作价值函数,然后在决策时选择动作价值即 值最大对应的动作即可。这样一来,策略和动作价值函数同时达到最优,相应的状态价值函数也是最优的,这就是 算法的思路。
算法更新公式如下:
而在时序差分方法中,状态价值函数的更新公式如下:
两者的更新方式都是基于时序差分的更新方法。不同的是,动作价值函数更新时是直接拿最大未来动作价值 来估计的,而在状态价值函数更新中相当于是拿对应的平均值来估计的。这就会导致这个估计相当于状态价值函数中的估计更不准确,一般称为 Q 值的过估计 ,当然这个过估计仅仅限于以 为基础的算法,不同的算法为了优化这个问题使用了不同的估计方式。
# Q 表格
算法的核心即为上面提到的更新公式,但是仍需要了解算法的相关概念, 表格和探索策略。
关于 表格,我们依旧沿用前面机器人寻找终点的问题,现在稍微更改条件:将网格变成 ,不再限制机器人的运动方向,可以向上、下、左、右任意移动,当然每次只能走一格,不能移除边界,奖励函数不变。
我们将机器人的位置当成状态,此时有 9 个状态,4 种动作 (分别对应上、下、左、右)。
而 Q 函数,即状态价值函数是输入状态和动作,输出一个值,由于这里的状态和动作都是离散的,因此可以用一个表格来表示,即 表格
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
表格的横和列对应状态和动作,数值表示对应的 值,比如最左上角的值表示 。在实践中,我们可以给所有的 预先设一个随机值,此处为了方便全部初始化为 。
值得注意的是,表格中终止状态对应的值必须为 ,比如此处的终止状态 对应的 , , , 必须为
,并且也不参与 值的更新。
现在我们讲讲 值的更新过程与前面涉及的状态价值更新类似。不同的是,状态价值的更新是蒙特卡洛方法, 值更新是时序差分方法。具体的做法是,让机器人自行在网格中走动,走到一个状态,就把对应的 值更新一次,将这个过程称为探索。
# 探索策略
理论上,直接根据 函数(即每次选择 值最大对应的动作)来探索是没有问题的。但是由于在探索的过程中 值也是估计出来的,然后还需要利用先前的估计值来更新 值(也就是自举的过程),换句话说,由于自举依赖于先前的估计值,因此这可能会导致估计出的价值函数存在某种程度上的偏差。
算法采用的探索策略名为 。该策略指智能体在探索过程中会以 的概率按照 函数执行动作,剩下 概率执行随机动作。通常 的值会设置的很小,例如 。因此通常在实践中, 的值还会随着时步的增长而衰减,比如从 衰减到 。
确切的说,以 的概率执行动作的过程称之为 利用 (exploitation) ,而以 的概率随机动作的过程称之为 探索 (exploration) 。探索的多少难以定论,这就是大多数强化学习情景中需要面临的探索 - 利用窘境 (exploration-exploitation dilemma)。我们需要在探索和利用之间做一个权衡,这与深度学习中的偏差 - 方差权衡 (Bias-Variance Tradeoff) 如出一辙。
算法的伪代码如下
初始化 Q 表,Q (s,a) 任意设定或为 0,终止状态对应 Q 值必须为 0 | |
for 回合数 = 1, M do: | |
初始化状态 s | |
for 时步 = 1, T do: | |
根据某种策略(如 ε-greedy 策略)选择动作 a | |
执行动作 a,观察奖励 r 和新状态 s' | |
根据更新公式更新策略 | |
更新 s ← s' | |
a ← 从 Q 表中基于当前策略选择的新动作 | |
end for | |
end for |
# Sarsa 算法
算法与 是非常类似,但是模式却不同的两类算法, 算法被认为是 Off-Policy 算法,而 算法则是 。
但在形式上,两个算法只是在 值的更新公式上有所不同, 算法使用如下更新公式
算法直接用下一个状态和动作对应的 值来作为估计值,而 算法则是用下一个状态对应的最大 值。
# 同策略与异策略
尽管 算法和 算法仅在一行更新公式上有所区别,但这两种算法代表的是截然不同的两类算法。我们注意到, 算法在训练的过程中当前策略来生成数据样本,并在其基础上进行更新。换句话说,策略评估和策略改进过程是基于相同的策略完成的,这就是 同策略算法 。相应地,像 算法这样从其他策略中获取样本然后利用它们来更新目标策略,我们称作 异策略算法 。
也就是说,异策略算法基本上是从经验池或者历史数据中进行学习的。这两类算法有着不同的优缺点,同策略相对来说更加稳定,但是效率较低。而异策略通常来说更加高效,但是需要让获取样本的策略和更新的策略具备一定的分布匹配条件,以避免偏差。
# Q-learning 算法实践
# 定义训练
强化学习训练会迭代很多个回合(),在每回合中,首先重置环境回到初始化的状态,智能体根据状态选择动作,然后环境反馈中下一个状态和对应的奖励,同时智能体会更新策略,直到回合结束。这其实就是马尔可夫决策过程中智能体与环境互动的过程,写成一段通用的代码如下:
for i_ep in range (train_eps): # 遍历每个回合 | |
# 重置环境,获取初始状态 | |
state = env.reset () # 重置环境,即开始新的回合 | |
while True: # 对于比较复杂的游戏可以设置每回合最大的步长,例如 while ep_step<100,即最大步长为 100。 | |
# 智能体根据策略采样动作 | |
action = agent.sample_action (state) # 根据算法采样一个动作 | |
# 与环境进行一次交互,得到下一个状态和奖励 | |
next_state, reward, terminated, _ = env.step (action) # 智能体将样本记录到经验池中 | |
agent.memory.push (state, action, reward, next_state, terminated) | |
# 智能体更新策略 | |
agent.update (state, action, reward, next_state, terminated) | |
# 更新状态 | |
state = next_state | |
# 如果终止则本回合结束 | |
if terminated: | |
break |
# 定义算法
强化学习中有几个要素,智能体、环境、经验池(经回放),在实践中也需要逐一定义这些要素。我们一般首先定义智能体,或者说算法,在 中一般定义为类即可。再考虑一下智能体在强化学习中主要负责哪些工作。
# 采样动作
首先在训练中需要采样动作与环境交互,我们可以定义一个类方法,命名为 sample_action ,如下:
class Agent: | |
def __init__(): | |
pass | |
def sample_action (self, state): | |
''' 采样动作,训练时用 | |
''' | |
self.sample_count += 1 | |
# epsilon 是会递减的,这里选择指数递减 | |
self.epsilon = self.epsilon_end + (self.epsilon_start - self.epsilon_end) * math.exp (- self.sample_count/self.epsilon_decay) | |
# e-greedy 策略 | |
if np.random.uniform (0, 1) > self.epsilon: | |
action = np.argmax (self.Q_table [str (state)]) # 选择 Q (s,a) 最大对应的动作 | |
else: | |
action = np.random.choice (self.n_actions) # 随机选择动作 | |
return action |
这里采用 策略,其中 会随着采样的步数指数衰减。 在 算法中还有一个重要的元素,即 表, 表的作用是输入状态和动作,输出一个即可,我们可以用一个二维的数组来表示,比如 Q_table [0][1] = 0.1 可以表示 (注意 里下标是从 开始)。而在我们的示例代码中用了一个默认字典来表示,如下:
self.Q_table = defaultdict (lambda: np.zeros (n_actions)) |
这样的好处是从数据结构上来说,默认字典是哈希表结构,二维数组是线性表结构,从哈希表拿出数据的速度会比线性表快。
# 预测动作
此外对于每个智能体在训练中和在测试中采取动作的方式一般是不一样的,因为在训练中需要增加额外的探索策略,而在测试中只需要输出
值对应最大的动作即可,如下:
class Agent: | |
def __init__(): | |
pass | |
def predict_action (self,state): | |
''' 预测或选择动作,测试时用 | |
''' | |
action = np.argmax (self.Q_table [str (state)]) | |
return action |
# 更新方法
所有强化学习算法的采样动作和预测动作方式几乎是比较固定的,对于每个智能体来说最核心的还是更新网络的方式,在 算法中的更新方式较为简单,而且不需要经验回放,如下:
def update (self, state, action, reward, next_state, terminated): | |
Q_predict = self.Q_table [str (state)][action] | |
if terminated: # 终止状态 | |
Q_target = reward | |
else: | |
Q_target = reward + self.gamma * np.max (self.Q_table [str (next_state)]) | |
self.Q_table [str (state)][action] += self.lr * (Q_target - Q_predict) |
其中 self.lr 就是更新公式中的 (学习率)。
# 定义环境
训练选用一个低难度的环境: CliffWalking-v0 (中文名 “悬崖寻路” )。如下图所示,整个环境中共有 48 个网格,其中黄色网格(标号为 36)为起点,绿色网格(标号为 47)为终点,红色的网格表示悬崖,智能体的目标是以最短的路径从起点到终点,并且避开悬崖。

在做强化学习算法时更重要的是要对环境本身的状态、动作和奖励了解。在本环境中,状态根据智能体所处网格的编号确定,动作分为上右下左,分别对应 。当智能体走到白色网格 (包括起点) 奖励为 ,到达终点获得奖励 0,走到边沿、悬崖或终点时结束本回合。
该环境由 OpenAI Gym 开发,它提供了一套标准化的环境,包括经典的控制理论问题和游戏,代码封装较好,只需要一行代码就能定义好环境,如下:
env = gym.make ('CliffWalking-v0') |
在 Gym 中我们可以通过以下方式获取环境的状态数和动作数:
n_states = env.observation_space.n # 状态数 | |
n_actions = env.action_space.n # 动作数 | |
print (f"状态数:{n_states}, 动作数:{n_actions}") |
# 设置参数
由于 算法的超参数(需要人工调整的参数)比较少,其中 (折扣因子)比较固定,设置在 到 之间,一般设置成 即可。而学习率 在本章节中设置的比较大,为 ,实际更复杂的环境和算法中学习率是小于 ,因为太大很容易发生过拟和的问题,只是本节的环境和算法都比较简单,为了收敛得更快所以设置较大。此外由于我们探索策略中的 是会随着采样步数衰减的,在实践过程中既不能让它衰减得太快也不能让它衰减得太慢,因此需要合理设置如下参数:
self.epsilon_start = 0.95 # e-greedy 策略中 epsilon 的初始值 | |
self.epsilon_end = 0.01 # e-greedy 策略中 epsilon 的最终值 | |
self.epsilon_decay = 200 # e-greedy 策略中 epsilon 的衰减率 |
# 开始训练
这里给出完整的训练代码
# -*- coding:utf--8 -*- | |
import numpy as np | |
import math | |
import torch | |
from collections import defaultdict | |
# 定义模型 | |
class Qlearning (object): | |
def __init__(self,cfg): | |
''' 智能体类 | |
Args: | |
cfg (class): 超参数类 | |
''' | |
self.n_actions = cfg.n_actions | |
self.exploration_type = 'e-greedy' # 探索策略如 e-greedy ,boltzmann ,softmax, ucb 等 | |
self.lr = cfg.lr | |
self.gamma = cfg.gamma | |
self.epsilon = cfg.epsilon_start | |
self.sample_count = 0 | |
self.epsilon_start = cfg.epsilon_start | |
self.epsilon_end = cfg.epsilon_end | |
self.epsilon_decay = cfg.epsilon_decay | |
self.Q_table = defaultdict (lambda: np.zeros (self.n_actions)) # 使用嵌套字典来表示 Q (s,a),并将指定所有的 Q_table 创建时, Q (s,a) 初始设置为 0 | |
def sample_action (self, state): | |
''' 以 e-greedy 策略训练时选择动作 | |
Args: | |
state (array): 状态 | |
Returns: | |
action (int): 动作 | |
''' | |
if self.exploration_type == 'e-greedy': | |
action = self._epsilon_greedy_sample_action (state) | |
else: | |
raise NotImplementedError | |
return action | |
def predict_action (self,state): | |
''' 预测动作 | |
Args: | |
state (array): 状态 | |
Returns: | |
action (int): 动作 | |
''' | |
if self.exploration_type == 'e-greedy': | |
action = self._epsilon_greedy_predict_action (state) | |
else: | |
raise NotImplementedError | |
return action | |
def _epsilon_greedy_sample_action (self, state): | |
''' | |
采用 epsilon-greedy 策略进行动作选择 | |
Args: | |
state (array): 状态 | |
Returns: | |
action (int): 动作 | |
''' | |
self.sample_count += 1 | |
# epsilon 值需要衰减,衰减方式可以是线性、指数等,以平衡探索和开发 | |
self.epsilon = self.epsilon_end + (self.epsilon_start - self.epsilon_end) * \ | |
math.exp (-1. * self.sample_count/self.epsilon_decay) | |
if np.random.uniform (0, 1) > self.epsilon: | |
action = np.argmax (self.Q_table [str (state)]) # 选择具有最大 Q 值的动作 | |
else: | |
action = np.random.choice (self.n_actions) # 随机选择一个动作 | |
return action | |
def _epsilon_greedy_predict_action (self,state): | |
''' | |
使用 epsilon-greedy 算法进行动作预测 | |
Args: | |
state (array): 状态 | |
Returns: | |
action (int): 动作 | |
''' | |
action = np.argmax (self.Q_table [str (state)]) | |
return action | |
def update (self, state, action, reward, next_state, done): | |
''' 更新模型 | |
Args: | |
state (array): 当前状态 | |
action (int): 当前动作 | |
reward (float): 当前奖励信号 | |
next_state (array): 下一个状态 | |
done (bool): 表示是否达到终止状态 | |
''' | |
Q_predict = self.Q_table [str (state)][action] | |
if done: # 终止状态 | |
Q_target = reward | |
else: | |
Q_target = reward + self.gamma * np.max (self.Q_table [str (next_state)]) | |
self.Q_table [str (state)][action] += self.lr * (Q_target - Q_predict) | |
def save_model (self,path): | |
''' | |
保存模型 | |
Args: | |
path (str): 模型存储路径 | |
''' | |
import dill | |
from pathlib import Path | |
# 确保存储路径存在 | |
Path (path).mkdir (parents=True, exist_ok=True) | |
torch.save ( | |
obj=self.Q_table, | |
f=path+"Qleaning_model.pkl", | |
pickle_module=dill | |
) | |
print ("Model saved!") | |
def load_model (self, path): | |
''' | |
根据模型路径导入模型 | |
Args: | |
fpath (str): 模型路径 | |
''' | |
import dill | |
self.Q_table =torch.load (f=path+'Qleaning_model.pkl',pickle_module=dill) | |
print ("Mode loaded!") | |
# 定义模型训练与测试 | |
def train (cfg, env, agent): | |
''' 训练 | |
''' | |
print ("开始训练!") | |
rewards = [] # 记录所有回合的奖励 | |
steps = [] | |
for i_ep in range (cfg.train_eps): | |
ep_reward = 0 # 一轮的累计奖励 | |
ep_step = 0 | |
state = env.reset (seed = cfg.seed) # 重置环境并获取初始状态 | |
for _ in range (cfg.max_steps): | |
ep_step += 1 | |
action = agent.sample_action (state) # 采样动作 | |
if cfg.new_step_api: | |
next_state, reward, terminated, truncated , info = env.step (action) # 更新环境并返回新状态、奖励、终止状态、截断标志和其他信息(使用 OpenAI Gym 的 new_step_api) | |
else: | |
next_state, reward, terminated, info = env.step (action) # 更新环境并返回新状态、奖励、终止状态和其他信息(使用 OpenAI Gym 的 old_step_api) | |
agent.update (state, action, reward, next_state, terminated) # 更新 agent | |
state = next_state # 更新状态 | |
ep_reward += reward # 增加奖励 | |
if terminated: | |
break | |
steps.append (ep_step) | |
rewards.append (ep_reward) | |
if (i_ep + 1) % 10 == 0: | |
print (f"回合:{i_ep+1}/{cfg.train_eps},奖励:{ep_reward:.2f}") | |
print ("完成训练!") | |
return {'rewards':rewards} | |
def test (cfg, env, agent): | |
print ("开始测试!") | |
rewards = [] # 记录所有回合的奖励 | |
steps = [] | |
for i_ep in range (cfg.test_eps): | |
ep_reward = 0 # 一轮的累计奖励 | |
ep_step = 0 | |
state = env.reset (seed = cfg.seed) # 重置环境并获取初始状态 | |
for _ in range (cfg.max_steps): | |
if cfg.render: | |
env.render () | |
ep_step += 1 | |
action = agent.predict_action (state) # 预测动作 | |
next_state, reward, terminated, truncated , info = env.step (action) | |
state = next_state # 更新状态 | |
ep_reward += reward # 增加奖励 | |
if terminated: | |
break | |
steps.append (ep_step) | |
rewards.append (ep_reward) | |
print (f"回合:{i_ep+1}/{cfg.test_eps},奖励:{ep_reward:.2f}") | |
print ("完成测试") | |
env.close () | |
return {'rewards':rewards} | |
# 定义环境 | |
import gymnasium as gym | |
import os | |
import random | |
def all_seed (env,seed = 1): | |
''' 万能的 seed 函数 | |
''' | |
env.reset (seed=seed) # env config | |
np.random.seed (seed) | |
random.seed (seed) | |
torch.manual_seed (seed) # config for CPU | |
torch.cuda.manual_seed (seed) # config for GPU | |
os.environ ['PYTHONHASHSEED'] = str (seed) # config for python scripts | |
# config for cudnn | |
torch.backends.cudnn.deterministic = True | |
torch.backends.cudnn.benchmark = False | |
torch.backends.cudnn.enabled = False | |
def env_agent_config (cfg): | |
env = gym.make (cfg.env_name) # 创建环境 | |
all_seed (env,seed=cfg.seed) | |
print (env.observation_space.shape) | |
n_states = env.observation_space.n | |
n_actions = env.action_space.n | |
print (f"状态空间维度:{n_states},动作空间维度:{n_actions}") | |
# 更新 n_states 和 n_actions 到 cfg 参数中 | |
setattr (cfg, 'n_states', n_states) | |
setattr (cfg, 'n_actions', n_actions) | |
setattr (cfg, 'action_space', env.action_space) | |
agent = Qlearning (cfg) | |
return env,agent | |
# 设置参数 | |
import matplotlib.pyplot as plt | |
import seaborn as sns | |
class Config: | |
def __init__(self) -> None: | |
## 通用参数 | |
self.env_name = "CliffWalking-v0" # name of environment | |
self.new_step_api = True # whether to use new step api of gym | |
self.wrapper = None # wrapper of environment | |
self.render = False # whether to render environment | |
self.render_mode = "human" # 渲染模式,"human" 或者 "rgb_array" | |
self.algo_name = "Qlearning" # name of algorithm | |
self.mode = "train" # train or test | |
self.mp_backend = "mp" # 多线程框架,ray 或者 mp (multiprocessing),默认 mp | |
self.seed = 1 # random seed | |
self.device = "cuda" # device to use | |
self.train_eps = 500 # number of episodes for training | |
self.test_eps = 10 # number of episodes for testing | |
self.eval_eps = 10 # number of episodes for evaluation | |
self.eval_per_episode = 5 # evaluation per episode | |
self.max_steps = 1000 # max steps for each episode | |
self.load_checkpoint = False | |
self.load_path = "tasks" # path to load model | |
self.show_fig = False # show figure or not | |
self.save_fig = True # save figure or not | |
## Qlearing 参数 | |
self.epsilon_start = 0.95 # epsilon 初始值 | |
self.epsilon_end = 0.01 # epsilon 终止值 | |
self.epsilon_decay = 300 # epsilon 衰减率 | |
self.gamma = 0.90 # 奖励折扣因子 | |
self.lr = 0.1 # 学习率 | |
def smooth (data, weight=0.9): | |
''' 用于平滑曲线,类似于 Tensorboard 中的 smooth 曲线 | |
''' | |
last = data [0] | |
smoothed = [] | |
for point in data: | |
smoothed_val = last * weight + (1 - weight) * point # 计算平滑值 | |
smoothed.append (smoothed_val) | |
last = smoothed_val | |
return smoothed | |
def plot_rewards (rewards,title="learning curve"): | |
sns.set_theme (style="whitegrid") | |
plt.figure () # 创建一个图形实例,方便同时多画几个图 | |
plt.title (f"{title}") | |
plt.xlim (0, len (rewards)) # 设置 x 轴的范围 | |
plt.xlabel ('episodes') | |
plt.plot (rewards, label='rewards') | |
plt.plot (smooth (rewards), label='smoothed') | |
plt.legend () | |
plt.show () | |
# 开始训练 | |
# 获取参数 | |
cfg = Config () | |
# 训练 | |
env, agent = env_agent_config (cfg) | |
res_dic = train (cfg, env, agent) | |
plot_rewards (res_dic ['rewards'], title=f"training curve on {cfg.device} of {cfg.algo_name} for {cfg.env_name}") | |
# 测试 | |
res_dic = test (cfg, env, agent) | |
plot_rewards (res_dic ['rewards'], title=f"testing curve on {cfg.device} of {cfg.algo_name} for {cfg.env_name}") # 画出结果 |
# 结果分析
根据代码输出的图表,我们发现训练曲线从 50 回合开始收敛,此时智能体学习到了最优策略。同时收敛值在 13 左右波动,波动的原因正是存在 0.01 的随机探索概率。
# 消融实验
为了探究 是随采样步数衰减好还是恒定不变好,我们可以做一个消融实验 (Ablation) ,设定 恒定为 0.1,如下
# 将初始值和最终值设置为一样,这样 epsilon 就不会衰减 | |
self.epsilon_start = 0.1 # e-greedy 策略中 epsilon 的初始值 | |
self.epsilon_end = 0.1 # e-greedy 策略中 epsilon 的最终值 | |
self.epsilon_decay = 200 # e-greedy 策略中 epsilon 的衰减率 |
再次训练,在输出的图像中能够发现,虽然曲线最后也能收敛,但是相对来说没那么稳定。在更复杂的环境中, 随着采样步数衰减会更好。
# 深度学习基础
前面章节主要介绍了传统强化学习的内容,但相关算法无法解决高纬度复杂问题,现在普遍流行将深度学习与强化学习结合,利用深度学习网络强大的拟合能力通过将状态、动作等作为输入,来估计对应的状态价值和动作价值等。
该章主要是对强化学习中用到的深度学习相关知识进行简要归纳,如果想了解深度学习的基础内容,可以参考: 李宏毅深度学习笔记
# 强化学习与深度学习
强化学习的问题可以拆分成两类问题,即预测和控制。预测的主要目的是根据环境的状态和动作来预测状态价值和动作价值,而控制的主要目的是根据状态价值和动作价值来选择动作。
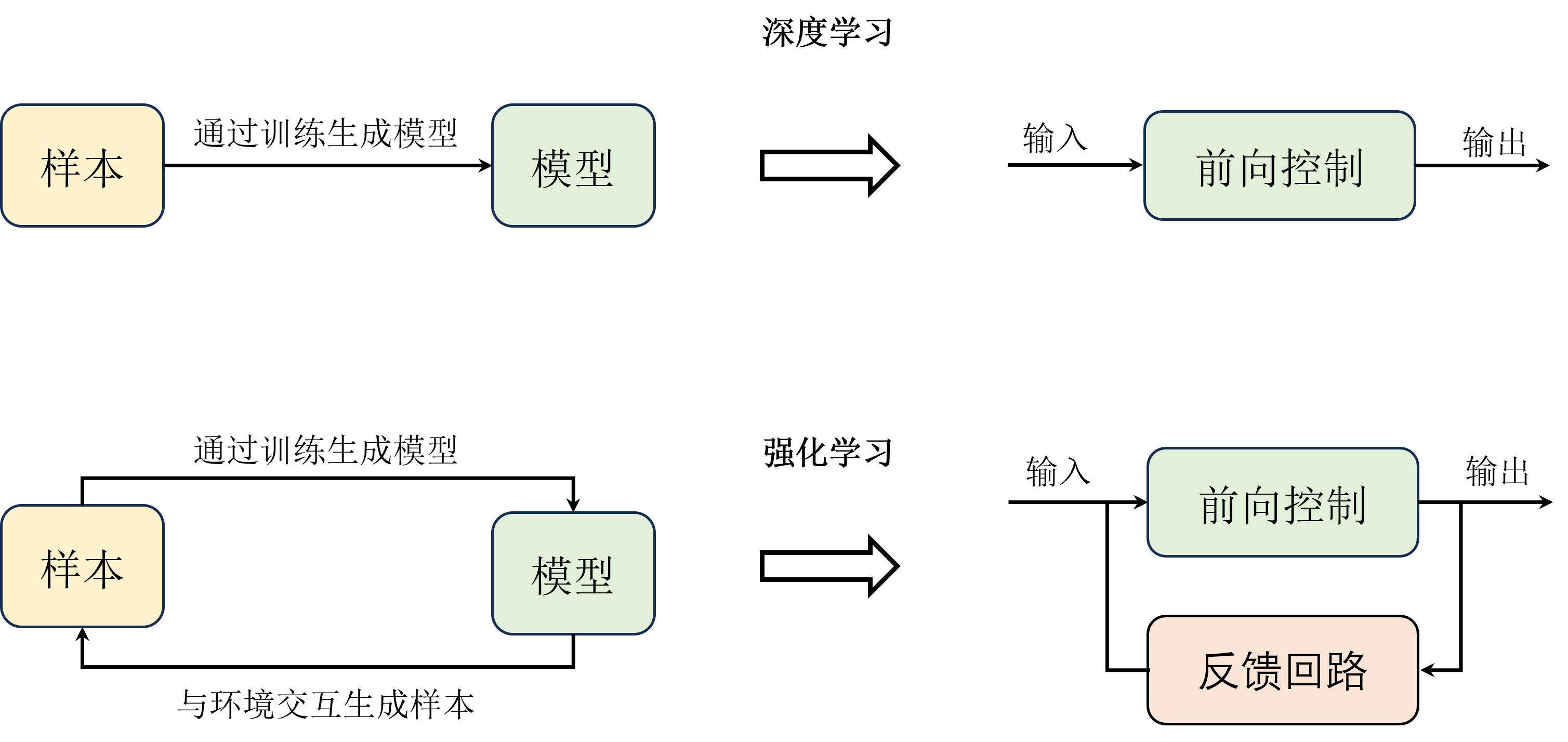
从训练模式上来看,深度学习和强化学习,尤其是结合了深度学习的深度强化学习,都是基于大量的样本来对相应算法进行迭代更新并且达到最优的,这个过程我们称之为训练。但与另外两者不同的是,强化学习是在交互中产生样本的,是一个产生样本、算法更新、再次产生样本、再次算法更新的动态循环训练过程,而不是一个准备样本、算法更新的静态训练过程。
除了训练生成模型之外,强化学习相当于在深度学习的基础上增加了一条回路,即继续与环境交互产生样本。这个回路就是一个典型的反馈系统机制,模型的输出一开始并不能达到预期的值,因此通过动态地不断与环境交互来产生一些反馈信息,从而训练出一个更好的模型。
# 线性回归
严格来说,线性模型并不是深度学习模型,而是传统的机器学习模型,但它是深度学习模型的基础,在深度学习中相当于单层的神经网络。在线性模型中,应用较为广泛的两个基础模型就是线性回归和逻辑回归,通常分别用于解决回归和分类问题,尽管后者也可以用来解决回归问题。
假设有 个特征,记为 ,需要预测的目标 表示为
其中 和 是模型参数, 是模型输出,也就是需要预测的值,通常使用 来表示 和 ,如
在这类问题中,这样的关系可以用模型来表述,我们的目标是求得一组最优的参数 ,使得该模型尽可能地能够根据 个特征准确预测对应的目标。
另外注意,这里是近似求解,因为几乎不可能找到一种模型能够完美拟合所有的样本,即找到最优解,甚至这个最优解不一定存在。因此,这类问题也普遍存在过拟合和欠拟合的问题,欠拟合指的是模型在训练集上表现就很差(可能在测试集中表现还行),而过拟合则是指在训练集上表现很好,但在测试集上表现很差。这两种情况都是不理想的,本质上都是陷入了局部最优解的问题,因此我们有时候需要一些方法来解决这个问题,比如正则化、数据增强等。
# 梯度下降
梯度下降是一种优化算法,主要用于解决机器学习中的参数优化问题。在机器学习中,我们通常需要找到一组模型参数,使得模型的预测误差(损失函数)最小。梯度下降通过迭代地调整模型参数,逐步减小损失函数的值,从而找到使损失函数最小化的参数值。基本思想如下
- 初始化参数:选择一个初始点或参数的初始值。
- 计算梯度:在当前点计算函数的梯度,即函数关于各参数的偏导数。梯度指向函数值增加最快的方向。
- 更新参数:按照负梯度方向更新参数,这样可以减少函数值。这个过程在神经网络中一般是以反向传播算法来实现的。
- 重复上述二三步骤,直到梯度趋近于 0 或者达到一定迭代次数。
梯度下降本质上是一种基于贪心思想的方法,它的泛化能力很强,能够基于任何可导的函数求解最优解。
# 逻辑回归
逻辑回归用来解决分类问题。在分类问题中,我们的目标是预测样本的类别,而不是预测一个连续的值。例如二分类问题,通常输出 1 和 0 等离散的数字来表示对应的类别。在形式上,逻辑回归和线性回归非常相似,就是在线性模型的后面增加一个 sigmoid 函数,我们一般称之为激活函数。
sigmoid 函数定义式为
sigmoid 函数可以将输入的任意实数映射到 (0,1) 的区间内,对其输出的值进行判断,例如小于 0.5 我们认为预测的是类别 0,反之是类别 1,这样一来通过梯度下降来求解模型参数就可以用于实现二分类问题了。注意,虽然逻辑回归只是在线性回归模型基础上增加了一个激活函数,但两个模型是完全不同的,包括损失函数等等。线性回归的损失函数是均方差损失,而逻辑回归模型一般是交叉熵损失,这两种损失函数在深度学习和深度强化学习中都很常见。
逻辑回归的主要优点在于增加了模型的非线性能力,同时模型的参数也比较容易求解,但是它也有一些缺点,例如它的非线性能力还是比较弱的,而且它只能解决二分类问题,不能解决多分类问题。在实际应用中,我们一般会将多个二分类问题组合成一个多分类问题,例如将 sigmoid 函数换成 softmax 回归函数等。
# 全连接网络
如下图所示,将线性层横向堆叠起来,前一层网络的所有神经元的输出都会输入到下一层的所有神经元中,这样就可以得到一个全连接网络。其中,每个线性层的输出都会经过一个激活函数(图中已略去),这样就可以增加模型的非线性能力。

我们把这样的网络叫做全连接网络(fully connected network),也称作多层感知机(multi-layer perceptorn,MLP),是最基础的深度神经网络模型。把神经网络模型中前一层的输入向量记为 ,其中第一层的输入也就是整个模型的输入可记为 ,每一个全连接层将前一层的输入映射到 ,也就是后一层的输入,具体定义为
其中 是权重矩阵, 为偏置矩阵,与线性模型类似,这两个参数我们通常看作一个参数 。 是激活函数,除了 sigmoid 函数之外,还包括 sofymax 函数、ReLU 函数和 tanh 函数等等激活函数。其中最常用的是 ReLU 函数 和 tanh 函数,前者将神经元也就是线性函数的输出映射到 (0,1),后者则映射到 (-1,1)。
在了解到神经网络前后层的关系之后,我们就可以表示一个 层的神经网络
第 1 层:
第 2 层:
第 层:
从上面的式子可以看出,神经网络模型的参数包括每一层的权重矩阵和偏置矩阵,也就是 ,这些参数都需要学习,我们需要找到一组参数使得神经网络模型的输出尽可能地接近真实值,这个过程就是神经网络的训练过程。同基础的线性模型类似,神经网络也可以通过梯度下降的方法来求解最优参数。
# 更高级的神经网络
# 卷积神经网络
卷积神经网络(convolutional neural network, CNN)适用于处理具有网格结构的数据,如图像(2D 网格像素点)或时间序列数据(1D 网格)等。在使用卷积神经网络的时候,我们需要注意以下几个主要特点:
- 局部感受野:传统的线性神经网络每个节点都与前一层的所有节点相连接。但在 CNN 中,我们使用小的局部感受野(例如 3x3 或 5x5 的尺寸),它只与前一层的一个小区域内的节点相连接。这可以减少参数数量,并使得网络能够专注于捕捉局部特征。
- 权重共享:在同一层的不同位置,卷积核的权重是共享的,这不仅大大减少了参数数量,还能帮助网络在图像的不同位置检测同样的特征。
- 池化层:池化层常常被插入在连续的卷积层之间,用来减少特征图的尺寸、减少参数数量并提高网络的计算效率。最常见的池化操作是最大池化(Max-Pooling),它将输入特征图划分为若干个小区域,并输出每个区域的最大值。
- 归一化和 Dropout:为了优化网络的性能和防止过拟合,可以在网络中添加归一化层(如 Batch Normalization)和 Dropout 。
# 循环神经网络
循环神经网络(recurrent neural network,RNN)适用于处理序列数据,也是最基础的一类时序网络。在强化学习中,循环神经网络常常被用来处理序列化的状态数据。但是基础的 RNN 结构很容易产生梯度消失或者梯度爆炸的问题,因此我们通常会使用一些改进的循环神经网络结构,例如 LSTM
和 GRU 等。LSTM 主要是通过引入门机制(输入门、遗忘门和输出门)来解决梯度消失的问题,它能够在长序列中维护更长的依赖关系。而 GRU 则是对 LSTM 的简化,它只有两个门(更新门和重置门),并且将记忆单元和隐藏状态合并为一个状态向量,性能与 LSTM
相当,但通常计算效率更高。
还有一种特殊的结构,叫做
Transformer 。虽然它也是为了处理序列数据而设计的,但是是一个完全不同的结构,不再依赖循环来处理序列,而是使用自注意机制 (self-attention mechanism) 来同时考虑序列中的所有元素。并且 Transformer 的设计特别适合并行计算,使得训练速度更快。自从被提出以后,Transformer 就被广泛应用于自然语言处理领域,例如 BERT,GPT 等模型。
# DQN 算法
本章介绍深度强化学习中的 DQN 算法,DQN(Deep Q-Network)算法是在 Q-learning 算法的基础上引入了深度神经网络来近似动作价值函数 ,从而能够处理高纬的状态空间。该算法除了用深度网络代替 Q 表之外,还引入了经验回放,目标网络等。
# 深度网络
在此之前,我们知道一个神经网络能够将输入向量 映射到输出向量
,这个映射过程可以用下式表示
某种意义上来说,神经网络就是一个函数,只不过不同于一般的数值函数,它的输入输出都是向量,并且拥有可以学习的参数 ,这些参数可以通过梯度下降的方式来优化,从而使得神经网络能够逼近任意函数。类似于 表,它也可以用来近似动作价值函数 ,即将状态向量 作为输入,并输出所有动作
对应的价值,如下
尽管神经网络和 表都可以用来近似动作价值函数 ,但是它们的形式是不一样的, 表是一个二维表格,而神经网络是一个实实在在的函数。因此, 表的局限性会更大一些,它只能处理离散的状态和动作空间,而神经网络则可以处理连续的状态和动作空间。例如在前面的寻路问题中, 表将每个位置看作不同的状态,但是如果需要获取到更加精细的位置,就需要更多的状态。
但神经网络可以输入连续值,因此只需要把每个维度的坐标看作一个输入,就可以处理高维的状态空间了。换句话说,神经网络只用了两个维度的输入就表示了原来 表中无穷多个状态,这就是神经网络的优势所在。因此,在 表中描述状态空间的时候一般用的是状态个数,而在神经网络中用的是状态维度。
另外注意,无论是 表还是 中的神经网络,它们输出的都是每个动作对应的 值,即预测,而不是直接输出动作。要想输出动作,就需要额外做一些处理,例如结合贪心算法选择 值最大对应的动作等,这就是控制过程。
虽然用神经网络替代 表看起来很容易,但是实际上也多了一项额外的参数,即神经网络的参数 ,此时需要用梯度下降的方法来求解。首先回顾一下 的算法更新公式
其中 表示期望的 值, 表示实际的 值, 表示学习率。在 算法中,由于没有额外参数,因此只需要直接一步步迭代更新 值即可,而在 算法中,我们使用神经网络来近似 函数,引入额外的网格参数 ,如下式
式中的 也可以写成 。在理想的收敛情况下,实际的 值应该接近于期望的 值,即最小化 和 之间的绝对差值。这个差值也就是 误差,也可写成损失函数的形式并用梯度下降的方式求解参数 ,如下式
由于 算法也是基于 更新的,因此依然需要判断终止状态,在 算法中也有同样的操作,如下式
从这个角度上来看,强化学习跟深度学习的训练方式其实是一样的,都是将样本喂入网络中,然后通过梯度下降的方式来更新网络参数,使得损失函数最小,即能够逼近真实的 值。而不同的地方在于,强化学习用于训练的样本(包括状态、动作和奖励等等)是与环境实时交互得到的,而深度学习则是事先准备好的。当然即便训练方式类似,这也并不代表强化学习和深度学习之间的区别就很小,本质上来讲强化学习和深度学习所要解决的问题是完全不同的,前者用于解决序列决策问题,后者用于解决静态问题例如回归、分类、识别等等。
# 经验回放
经验回放是所有 off-policy 算法中都会用到的一个技巧。在强化学习中,智能体在与环境的实时交互中得到样本并训练,而在深度学习中,训练集是提前准备好的,每次训练的样本从训练集中随机抽取,这样的样本是相互独立的,这与强化学习不同,强化学习由于实时获取,迭代的样本之间相互关联。
由此引入经验回放, 算法训练的方式就是把每次通过与环境交互一次的样本直接喂入网络中训练。而在 中,我们会把每次与环境交互得到的样本都存储在一个经验回放中,然后每次从经验池中随机抽取一批样本来训练网络。
这样做的好处是,首先每次迭代的样本都是从经验池中随机抽取的,因此每次迭代的样本都是近似独立同分布的,这样就满足了梯度下降法的假设。其次,经验池中的样本是从环境中实时交互得到的,因此每次迭代的样本都是相互关联的,这样的方式相当于是把每次迭代的样本都进行了一个打乱的操作,这样也能够有效地避免训练的不稳定性。

当然,与深度学习不同的是,经验回放的容量是需要有一定的容量限制的。本质上是因为在深度学习中我们拿到的样本都是事先准备好的,即都是很好的样本,但是在强化学习中样本是由智能体生成的,在训练初期智能体生成的样本虽然能够帮助它朝着更好的方向收敛,但是在训练后期这些前期产生的样本相对来说质量就不是很好了,此时把这些样本喂入智能体的深度网络中更新反而影响其稳定。这就好比我们在小学时积累到的经验,会随着我们逐渐长大之后很有可能就变得不是很适用了,所以经验回放的容量不能太小,太小了会导致收集到的样本具有一定的局限性,也不能太大,太大了会失去经验本身的意义。
# 目标网格
在 算法中还有一个重要的技巧,即使用了一个每隔若干步才更新的目标网络。如下图 所示,目标网络和当前网络结构都是相同的,都用于近似 值,在实践中每隔若干步才把每步更新的当前网络参数复制给目标网络,这样做的好处是保证训练的稳定,避免 值的估计发散。

同时在计算损失函数的时候,使用的是目标网络来计算 的期望值,如下式
使用目标网络可以防止从经验回放中提取到的连续样本导致 值被过估计而使 值发散的情况。
# DQN 算法实践
DQN 算法的伪代码如下
初始化回放记忆 D,容量为 N | |
初始化行动值函数 Q 用随机权重 θ | |
初始化目标行动值函数 \(\hat {Q}\) 用权重 \(\theta^- = \theta\) | |
观察初始状态 \(s\) | |
for episode = 1, M do | |
初始化随机过程 \(N\) 用于行动选择 | |
接收初始状态 \(s\) | |
for t = 1, T do | |
以 ε 概率随机选择一个行动 \(a_t\) | |
否则选择 \(a_t = \arg\max_a Q (s,a; \theta)\) | |
执行行动 \(a_t\),观察奖励 \(r_t\) 和新状态 \(s_{t+1}\) | |
将转换 \((s_t, a_t, r_t, s_{t+1})\) 存储在 D 中 | |
从 D 中随机抽取一个小批量转换 | |
对于每个转换,计算目标 Q 值: | |
\(y_j = | |
\begin {cases} | |
r_j & \mbox {如果 } s_{j+1} \mbox { 是终止状态} \\ | |
r_j + \gamma \max_{a'} \hat {Q}(s_{j+1}, a'; \theta^-) & \mbox {其他情况} | |
\end {cases}\) | |
对于这个小批量执行梯度下降步骤来更新网络参数 \(\theta\) | |
每 C 步复制 Q 网络到目标网络,即 \(\theta^- = \theta\) | |
end for | |
end for |
# 定义模型
定义两个神经网路,即当前网络和目标网络,由于这两个网络结构相同,这里只用一个 类来定义,如下
class MLP (nn.Module): # 所有网络必须继承 nn.Module 类,这是 PyTorch 的特性 | |
def __init__(self, input_dim,output_dim,hidden_dim=128): | |
super (MLP, self).__init__() | |
# 定义网络的层,这里都是线性层 | |
self.fc1 = nn.Linear (input_dim, hidden_dim) # 输入层 | |
self.fc2 = nn.Linear (hidden_dim,hidden_dim) # 隐藏层 | |
self.fc3 = nn.Linear (hidden_dim, output_dim) # 输出层 | |
def forward (self, x): | |
# 各层对应的激活函数 | |
x = F.relu (self.fc1 (x)) | |
x = F.relu (self.fc2 (x)) | |
return self.fc3 (x) # 输出层不需要激活函数 |
这里定义了一个三层的全连接网络,输入维度就是状态数,输出维度就是动作数,中间的隐藏层采用最常用的 激活函数。用 的 类来定义网络,这是
的特性,所有网络都必须继承这个类。在 中,我们只需要定义网络的前向传播,即 函数,反向传播的过程 会自动完成,这也是 的特性。
# 经验回放
经验回放的功能主要实现缓存样本和取出样本两个功能,实现经验回放的方式有很多,这里给一个参考代码
class ReplayBuffer: | |
def __init__(self, capacity): | |
self.capacity = capacity # 经验回放的容量 | |
self.buffer = [] # 用列表存放样本 | |
self.position = 0 # 样本下标,便于覆盖旧样本 | |
def push (self, state, action, reward, next_state, done): | |
''' 缓存样本 | |
''' | |
if len (self.buffer) < self.capacity: # 如果样本数小于容量 | |
self.buffer.append (None) | |
self.buffer [self.position] = (state, action, reward, next_state, done) | |
self.position = (self.position + 1) % self.capacity | |
def sample (self, batch_size): | |
''' 取出样本,即采样 | |
''' | |
batch = random.sample (self.buffer, batch_size) # 随机采出小批量转移 | |
state, action, reward, next_state, done = zip (*batch) # 解压成状态,动作等 | |
return state, action, reward, next_state, done | |
def __len__(self): | |
''' 返回当前样本数 | |
''' | |
return len (self.buffer) |
# 定义智能体
代码中的两个网络就是前面所定义的全连接网络,输入为状态维度,输出则是动作维度。这里我们还定义了一个优化器,用来更新网络参数。在 算法中采样动作和预测动作跟 是一样的,其中采样动作使用的是 策略,便于在训练过程中探索,而测试只需要检验模型的性能,因此不需要探索,只需要单纯的进行 预测即可,即选择最大值对应的动作。
class Agent: | |
def __init__(self): | |
# 定义当前网络 | |
self.policy_net = MLP (state_dim,action_dim).to (device) | |
# 定义目标网络 | |
self.target_net = MLP (state_dim,action_dim).to (device) | |
# 将当前网络参数复制到目标网络中 | |
self.target_net.load_state_dict (self.policy_net.state_dict ()) | |
# 定义优化器 | |
self.optimizer = optim.Adam (self.policy_net.parameters (), lr=learning_rate) | |
# 经验回放 | |
self.memory = ReplayBuffer (buffer_size) | |
self.sample_count = 0 # 记录采样步数 | |
def sample_action (self,state): | |
''' 采样动作,主要用于训练 | |
''' | |
self.sample_count += 1 | |
# epsilon 随着采样步数衰减 | |
self.epsilon = self.epsilon_end + (self.epsilon_start - self.epsilon_end) * math.exp (-1. * self.sample_count/self.epsilon_decay) | |
if random.random () > self.epsilon: | |
with torch.no_grad (): # 不使用梯度 | |
state = torch.tensor (np.array (state), device=self.device, dtype=torch.float32).unsqueeze (dim=0) | |
q_values = self.policy_net (state) | |
action = q_values.max (1)[1].item () # choose action corresponding to the maximum q value | |
else: | |
action = random.randrange (self.action_dim) | |
def predict_action (self,state): | |
''' 预测动作,主要用于测试 | |
''' | |
with torch.no_grad (): | |
state = torch.tensor (np.array (state), device=self.device, dtype=torch.float32).unsqueeze (dim=0) | |
q_values = self.policy_net (state) | |
action = q_values.max (1)[1].item () # choose action corresponding to the maximum q value | |
return action | |
def update (self): | |
pass |
# 算法更新
算法更新本质上与 区别不大。由于采用小批量随机梯度下降,当经验回放不满足批大小时选择不更新,这实际上是工程性问题。然后在更新时取出样本,并转换成 的张量,便于我们用 计算。接着计算 值的估计值和实际值,并得到损失函数。在得到损失函数并更新参数时,在代码上会有一个固定的写法,即梯度清零,反向传播和更新优化器的过程,跟在深度学习中的写法是一样的,最后需要定期更新一下目标网络,即每隔 步复制参数到目标网络。
def update (self, share_agent=None): | |
# 当经验回放中样本数小于更新的批大小时,不更新算法 | |
if len (self.memory) < self.batch_size: # when transitions in memory donot meet a batch, not update | |
return | |
# 从经验回放中采样 | |
state_batch, action_batch, reward_batch, next_state_batch, done_batch = self.memory.sample ( | |
self.batch_size) | |
# 转换成张量(便于 GPU 计算) | |
state_batch = torch.tensor (np.array (state_batch), device=self.device, dtype=torch.float) | |
action_batch = torch.tensor (action_batch, device=self.device).unsqueeze (1) | |
reward_batch = torch.tensor (reward_batch, device=self.device, dtype=torch.float).unsqueeze (1) | |
next_state_batch = torch.tensor (np.array (next_state_batch), device=self.device, dtype=torch.float) | |
done_batch = torch.tensor (np.float32 (done_batch), device=self.device).unsqueeze (1) | |
# 计算 Q 的实际值 | |
q_value_batch = self.policy_net (state_batch).gather (dim=1, index=action_batch) # shape (batchsize,1),requires_grad=True | |
# 计算 Q 的估计值,即 r+\gamma Q_max | |
next_max_q_value_batch = self.target_net (next_state_batch).max (1)[0].detach ().unsqueeze (1) | |
expected_q_value_batch = reward_batch + self.gamma * next_max_q_value_batch* (1-done_batch) | |
# 计算损失 | |
loss = nn.MSELoss ()(q_value_batch, expected_q_value_batch) | |
# 梯度清零,避免在下一次反向传播时重复累加梯度而出现错误。 | |
self.optimizer.zero_grad () | |
# 反向传播 | |
loss.backward () | |
# clip 避免梯度爆炸 | |
for param in self.policy_net.parameters (): | |
param.grad.data.clamp_(-1, 1) | |
# 更新优化器 | |
self.optimizer.step () | |
# 每 C (target_update) 步更新目标网络 | |
if self.sample_count % self.target_update == 0: | |
self.target_net.load_state_dict (self.policy_net.state_dict ()) |
# 定义环境
本次使用 OpenAI Gym 平台开发的环境 Cart Pole ,目标是持续左右推动让摇杆一直不倒。
环境的状态数是 4, 动作数是 2。 Cart Pole 的状态包括推车的位置(范围是 -4.8
到 4.8 )、速度(范围是负无穷大到正无穷大)、杆的角度(范围是 -24 度 到 24 度)和角速度(范围是负无穷大到正无穷大), 这几个状态都是连续的值,也就是前面所说的连续状态空间。
环境的奖励设置是每个时步下能维持杆不到就给一个 +1 的奖励,因此理论上在最优策略下这个环境是没有终止状态的,因为最优策略下可以一直保持杆不倒。由于基于 的算法都必须要求环境有一个终止状态,这里设定如果能在两百个时步以内坚持杆不到就近似说明学到了一个不错的策略。
# 设置参数
与 算法相比,除了 , 折扣因子以及学习率之外多了三个超参数,即经验回放的容量、批大小和目标网络更新频率。注意这里学习率在更复杂的环境中一般会设置得比较小,经验回放的容量是一个比较经验性的参数,根据实际情况适当调大即可,不需要额外花太多时间调。批大小也比较固定,一般都在 64,128,256,512 中间取值,目标网络更新频率会影响智能体学得快慢,但一般不会导致学不出来。总之,DQN 算法相对来说是深度强化学习的一个稳定且基础的算法,只要适当调整学习率都能让智能体学出一定的策略。
self.epsilon_start = 0.95 # epsilon 起始值 | |
self.epsilon_end = 0.01 # epsilon 终止值 | |
self.epsilon_decay = 500 # epsilon 衰减率 | |
self.gamma = 0.95 # 折扣因子 | |
self.lr = 0.0001 # 学习率 | |
self.buffer_size = 100000 # 经验回放容量 | |
self.batch_size = 64 # 批大小 | |
self.target_update = 4 # 目标网络更新频率 |
# 开始训练
训练代码会在根目录下的子目录 utils 导入相关类,此处注释掉了导入相关代码,并将 utils 目录下用到的类直接放到训练代码中。代码按照实践步骤进行分段,完整代码如下
# -*- coding:utf--8 -*- | |
# utils.utils 下相关类 | |
import os | |
import random | |
import numpy as np | |
import seaborn as sns | |
import matplotlib.pyplot as plt | |
import torch | |
from IPython.display import clear_output | |
def all_seed (seed: int = 0): | |
''' 设置随机种子 | |
''' | |
if seed == 0: | |
return | |
np.random.seed (seed) | |
random.seed (seed) | |
torch.manual_seed (seed) # config for CPU | |
torch.cuda.manual_seed (seed) # config for GPU | |
os.environ ['PYTHONHASHSEED'] = str (seed) # config for python scripts | |
# config for cudnn | |
torch.backends.cudnn.deterministic = True | |
torch.backends.cudnn.benchmark = False | |
torch.backends.cudnn.enabled = False | |
def smooth (data: list, weight: float = 0.9): | |
''' 用于平滑曲线,类似于 Tensorboard 中的 smooth 曲线 | |
''' | |
last = data [0] | |
smoothed = [] | |
for point in data: | |
smoothed_val = last * weight + (1 - weight) * point # 计算平滑值 | |
smoothed.append (smoothed_val) | |
last = smoothed_val | |
return smoothed | |
def plot_rewards (frames, rewards, device = 'cpu', algo_name = 'PPO', env_id= 'Pendulum-v1', tag='train'): | |
''' 画图 | |
''' | |
sns.set_theme (style="darkgrid") | |
clear_output (True) | |
plt.figure () # 创建一个图形实例,方便同时多画几个图 | |
plt.title (f"{tag} ing curve on {device} of {algo_name} for {env_id}") | |
plt.xlabel ('frames') | |
plt.plot (frames, rewards, label='rewards') | |
plt.plot (frames, smooth (rewards), label='smoothed rewards') | |
plt.legend () | |
plt.show () | |
def plot_losses (frames, losses, device = 'cpu', algo_name = 'PPO', env_id= 'Pendulum-v1', tag='train'): | |
''' 画图 | |
''' | |
sns.set_theme (style="darkgrid") | |
clear_output (True) | |
plt.figure () # 创建一个图形实例,方便同时多画几个图 | |
plt.title (f"{tag} ing curve on {device} of {algo_name} for {env_id}") | |
plt.xlabel ('frames') | |
plt.plot (frames, losses, label='losses') | |
plt.plot (frames, smooth (losses), label='smoothed losses') | |
plt.legend () | |
plt.show () | |
# 定义模型 | |
import torch.nn as nn | |
import torch.nn.functional as F | |
class MLP (nn.Module): | |
def __init__(self, state_dim,action_dim,hidden_dim=128): | |
""" 初始化 q 网络,为全连接网络 | |
""" | |
super (MLP, self).__init__() | |
self.fc1 = nn.Linear (state_dim, hidden_dim) # 输入层 | |
self.fc2 = nn.Linear (hidden_dim,hidden_dim) # 隐藏层 | |
self.fc3 = nn.Linear (hidden_dim, action_dim) # 输出层 | |
def forward (self, x): | |
# 各层对应的激活函数 | |
x = F.relu (self.fc1 (x)) | |
x = F.relu (self.fc2 (x)) | |
return self.fc3 (x) | |
# 定义经验回放 | |
import random | |
from collections import deque | |
class ReplayBuffer (object): | |
def __init__(self, capacity: int) -> None: | |
self.capacity = capacity | |
self.buffer = deque (maxlen=self.capacity) | |
def push (self,transitions): | |
''' 存储 transition 到经验回放中 | |
''' | |
self.buffer.append (transitions) | |
def sample (self, batch_size: int, sequential: bool = False): | |
if batch_size > len (self.buffer): # 如果批量大小大于经验回放的容量,则取经验回放的容量 | |
batch_size = len (self.buffer) | |
if sequential: # 顺序采样 | |
rand = random.randint (0, len (self.buffer) - batch_size) | |
batch = [self.buffer [i] for i in range (rand, rand + batch_size)] | |
return zip (*batch) | |
else: # 随机采样 | |
batch = random.sample (self.buffer, batch_size) | |
return zip (*batch) | |
def __len__(self): | |
''' 返回当前存储的量 | |
''' | |
return len (self.buffer) | |
# 定义智能体 | |
import torch | |
import torch.optim as optim | |
import math | |
import numpy as np | |
class DQN: | |
def __init__(self,model,memory,cfg): | |
self.action_dim = cfg.action_dim | |
self.device = torch.device (cfg.device) | |
self.gamma = cfg.gamma # 奖励的折扣因子 | |
# e-greedy 策略相关参数 | |
self.sample_count = 0 # 用于 epsilon 的衰减计数 | |
self.epsilon_start = cfg.epsilon_start | |
self.epsilon_end =cfg.epsilon_end | |
self.epsilon_decay = cfg.epsilon_decay | |
self.batch_size = cfg.batch_size | |
# 当前网络和目标网络 | |
self.policy_net = model.to (self.device) | |
self.target_net = model.to (self.device) | |
# 复制参数到目标网络 | |
for target_param, param in zip (self.target_net.parameters (),self.policy_net.parameters ()): | |
target_param.data.copy_(param.data) | |
self.optimizer = optim.Adam (self.policy_net.parameters (), lr=cfg.lr) # 优化器 | |
self.memory = memory # 经验回放 | |
def sample_action (self, state): | |
''' 采样动作 | |
''' | |
self.sample_count += 1 | |
# epsilon 指数衰减 | |
self.epsilon = self.epsilon_end + (self.epsilon_start - self.epsilon_end) * \ | |
math.exp (-1. * self.sample_count/self.epsilon_decay) | |
if random.random () > self.epsilon: | |
with torch.no_grad (): | |
state = torch.tensor (state, device=self.device, dtype=torch.float32).unsqueeze (dim=0) | |
q_values = self.policy_net (state) | |
action = q_values.max (1)[1].item () # choose action corresponding to the maximum q value | |
else: | |
action = random.randrange (self.action_dim) | |
return action | |
@torch.no_grad () # 不计算梯度,该装饰器效果等同于 with torch.no_grad (): | |
def predict_action (self, state): | |
''' 预测动作 | |
''' | |
state = torch.tensor (state, device=self.device, dtype=torch.float32).unsqueeze (dim=0) | |
q_values = self.policy_net (state) | |
action = q_values.max (1)[1].item () # choose action corresponding to the maximum q value | |
return action | |
def update (self): | |
if len (self.memory) < self.batch_size: # 当经验回放中不满足一个批量时,不更新策略 | |
return | |
# 从经验回放中随机采样一个批量的样本 | |
states, actions, rewards, next_states, dones = self.memory.sample ( | |
self.batch_size) | |
# 将数据转换为 tensor | |
states = torch.tensor (np.array (states), device=self.device, dtype=torch.float) # [batch_size, state_dim] | |
actions = torch.tensor (actions, device=self.device).unsqueeze (1) # [batch_size, 1] | |
rewards = torch.tensor (rewards, device=self.device, dtype=torch.float).unsqueeze (1) # [batch_size, 1] | |
next_states = torch.tensor (np.array (next_states), device=self.device, dtype=torch.float) # [batch_size, state_dim] | |
dones = torch.tensor (np.float32 (dones), device=self.device).unsqueeze (1) # [batch_size,1] | |
# 计算当前状态 (s_t,a) 对应的 Q 值 | |
q_values = self.policy_net (states).gather (dim=1, index=actions) | |
# 计算下一时刻的状态 (s_t_,a) 对应的 Q 值,注意需要 detach (),因为不需要计算梯度 | |
next_q_values_max = self.target_net (next_states).max (1)[0].detach ().unsqueeze (1) | |
# 计算期望的 Q 值,对于终止状态,此时 dones [0]=1, 对应的 expected_q_value 等于 reward | |
expected_q_values = rewards + self.gamma * next_q_values_max * (1-dones) # [batch_size, 1] | |
# 计算均方根损失 | |
loss = nn.MSELoss ()(q_values, expected_q_values) | |
# 优化更新模型 | |
self.optimizer.zero_grad () | |
loss.backward () | |
# clip 防止梯度爆炸 | |
for param in self.policy_net.parameters (): | |
param.grad.data.clamp_(-1, 1) | |
self.optimizer.step () | |
# 定义训练 | |
# from utils.utils import plot_rewards | |
def train (cfg, env, agent): | |
''' 训练 | |
''' | |
rewards = [] # 记录所有回合的奖励 | |
for i_ep in range (cfg.train_eps): | |
ep_reward = 0 # 记录一回合内的奖励 | |
ep_step = 0 | |
state, info = env.reset (seed = cfg.seed) # 重置环境,返回初始状态 | |
for _ in range (cfg.max_steps): | |
ep_step += 1 | |
action = agent.sample_action (state) # 选择动作 | |
next_state, reward, terminated, truncated , info = env.step (action) # 更新环境,返回 transition | |
agent.memory.push ((state, action, reward, next_state, terminated)) # 保存 transition | |
state = next_state # 更新下一个状态 | |
agent.update () # 更新智能体 | |
ep_reward += reward # 累加奖励 | |
if terminated: | |
break | |
if (i_ep + 1) % cfg.target_update == 0: # 智能体目标网络更新 | |
agent.target_net.load_state_dict (agent.policy_net.state_dict ()) | |
rewards.append (ep_reward) | |
print (f"rewards: {rewards}") | |
# if (i_ep + 1) % 10 == 0: | |
# print (f"回合:{i_ep+1}/{cfg.train_eps},奖励:{ep_reward:.2f},Epislon:{agent.epsilon:.3f}") | |
env.close () | |
plot_rewards (range (len (rewards)), rewards, tag='train') | |
return {'rewards':rewards} | |
def test (cfg, env, agent): | |
rewards = [] # 记录所有回合的奖励 | |
for i_ep in range (cfg.test_eps): | |
ep_reward = 0 # 记录一回合内的奖励 | |
ep_step = 0 | |
state, info = env.reset (seed = cfg.seed) # 重置环境,返回初始状态 | |
for _ in range (cfg.max_steps): | |
ep_step+=1 | |
action = agent.predict_action (state) # 选择动作 | |
next_state, reward, terminated, truncated, info = env.step (action) # 更新环境,返回 transition | |
state = next_state # 更新下一个状态 | |
ep_reward += reward # 累加奖励 | |
if terminated: | |
break | |
rewards.append (ep_reward) | |
# print (f"回合:{i_ep+1}/{cfg.test_eps},奖励:{ep_reward:.2f}") | |
env.close () | |
plot_rewards (range (len (rewards)), rewards, tag='test') | |
return {'rewards':rewards} | |
# 定义环境 | |
import gymnasium as gym | |
import os | |
# from utils.utils import all_seed | |
def env_agent_config (cfg): | |
env = gym.make (cfg.env_id) # 创建环境 | |
all_seed (seed=cfg.seed) | |
state_dim = env.observation_space.shape [0] | |
action_dim = env.action_space.n | |
print (f"状态空间维度:{state_dim},动作空间维度:{action_dim}") | |
setattr (cfg,"state_dim",state_dim) # 更新 state_dim 到 cfg 参数中 | |
setattr (cfg,"action_dim",action_dim) # 更新 action_dim 到 cfg 参数中 | |
model = MLP (state_dim, action_dim, hidden_dim = cfg.hidden_dim) # 创建模型 | |
memory = ReplayBuffer (cfg.memory_capacity) | |
agent = DQN (model,memory,cfg) | |
return env,agent | |
# 设置参数 | |
import matplotlib.pyplot as plt | |
import seaborn as sns | |
class Config: | |
def __init__(self) -> None: | |
self.algo_name = 'DQN' # 算法名称 | |
self.env_id = 'CartPole-v1' # 环境 id | |
self.seed = 1 # 随机种子,便于复现,0 表示不设置 | |
self.train_eps = 100 # 训练的回合数 | |
self.test_eps = 20 # 测试的回合数 | |
self.max_steps = 200 # 每个回合的最大步数,超过该数则游戏强制终止 | |
self.gamma = 0.95 # 折扣因子 | |
self.epsilon_start = 0.95 # e-greedy 策略中初始 epsilon | |
self.epsilon_end = 0.01 # e-greedy 策略中的终止 epsilon | |
self.epsilon_decay = 500 # e-greedy 策略中 epsilon 的衰减率 | |
self.memory_capacity = 100000 # 经验回放池的容量 | |
self.hidden_dim = 256 # 神经网络的隐藏层维度 | |
self.batch_size = 64 # 批次大小 | |
self.target_update = 4 # 目标网络的更新频率 | |
self.lr = 0.0001 # 学习率 | |
self.device = torch.device ("cuda" if torch.cuda.is_available () else "cpu") # 检测 gpu | |
# 获取参数 | |
cfg = Config () | |
# 训练 | |
env, agent = env_agent_config (cfg) | |
res_dic = train (cfg, env, agent) | |
# 测试 | |
res_dic = test (cfg, env, agent) |
在训练输出的图表中显示,环境每回合的最大步数是 200 ,对应的最大奖励也为 200,可以看出,智能体确实学到了一个最优的策略,即达到收敛。
# DQN 算法进阶
# Double DQN 算法
Double DQN 算法通过引入两个网络用于解决 值过估计的问题。DQN 算法分类于 2013 年和 2015 年提出了两个版本,后者就是目前较为成熟的 Nature DQN 版本,前者只是在 上引入深度神经网络,没有额外的技巧,而 Double DQN 算法在这之间被提出,因此 Nature DQN 在发表时也借鉴了 Double DQN 的思想。
先回顾一下 DQN 算法的更新公式:
其中 是估计值,这里的 指的是目标网络。即直接拿目标网络中各个动作对应的最大 值来当作估计值,这样会存在过估计的问题。为解决这个问题,Double DQN 采用了一种思路:先在当前网络中找出最大 值对应的动作,然后再将这个动作代入到目标网络中去计算 值。这样做相当于是把动作选择和动作评估这两个过程分离开来,从而减轻了过估计问题,两个步骤如下式
注意,虽然 Double DQN 算法和 Nature DQN 算法都用了两个网络,但实际上 Double DQN 算法训练方式是略有不同的。Double DQN 并不是每隔 步复制参数到目标网络,而是每次随机选择其中一个网络选择动作进行更新。假设两个网络分别为 和 ,那么在更新 的时候就用把 当作目标网络估计动作值,同时 也是用来选择动作的,如下式,反之亦然。
但其实这种训练方式的效果跟单纯每隔 步复制参数到目标网络的方式差不多,而且后者更加简单,所以实践中一般都是采用后者。
# Dueling DQN 算法
Double DQN 算法中通过改进目标 值的计算优化算法,而在 Dueling DQN 算法中则是通过优化神经网络的结构来优化算法。
在 DQN 算法中所使用的最基础网络结构是一个全连接网络,包含一个输入层、一个隐藏层和输出层。输入层的维度为状态的维度,输出层的维度为动作的维度。而 Dueling DQN 算法在输出层之前分流(dueling)出了两层,一个是优势层(advantage layer),用于估计每个动作带来的优势,输出维度为动作数一个是价值层(value layer),用于估计每个状态的价值,输出维度为 1 。
在 DQN 算法中我们用 表示 一个 网络,而在这里优势层可以表示为
,这里 表示共享隐藏层的参数, 表示优势层自己这部分的参数,相应地价值层可以表示为 。这样 Dueling DQN 算法中网络结构可表示为下式
另外会对优势层做一个中心化处理,即减掉均值,如下式
总的来讲,Dueling DQN 算法在某些情况下相对于 DQN 是有好处的,因为它分开评估每个状态的价值以及某个状态下采取某个动作的 值。当某个状态下采取一些动作对最终的回报都没有多大影响时,这个时候 Dueling DQN 这种结构的优越性就体现出来了。或者说,它使得目标值更容易计算,因为通过使用两个单独的网络,我们可以隔离每个网络输出上的影响,并且只更新适当的子网络,这有助于降低方差并提高学习鲁棒性。
# Noisy DQN 算法
Noisy DQN 算法也是通过优化网络结构的方法来提升 DQN 算法的性能,但与 Dueling DQN 算法不同的是,它的目的并不是为了提高 值的估计,而是增强网络的探索能力。
Noisy DQN 算法其实是在 DQN 算法基础上在神经网络中引入了噪声层来提高网络性能的,即将随机性应用到神经网络中的参数或者说权重,增加了 网络对于状态和动作空间的探索能力,从而提高收敛速度和稳定性。在实践上也比较简单,就是通过添加随机性参数到神经网络的线性层,对应的 值则可以表示为 ,注意不要把这里的 跟 策略中的 混淆了。虽然都叫做 ,但这里 是由高斯分布生成的总体分类噪声参数。
# PER DQN 算法
在 DQN 算法章节中我们讲到经验回放,从另一个角度来说也是为了优化深度网络中梯度下降的方式,或者说网络参数更新的方式。在 PER DQN 算法中,进一步优化了经验回放的设计从而提高模型的收敛能力和鲁棒性。PER 可以翻译为优先经验回放(prioritized experience replay),跟数据结构中优先队列与普通队列一样,会在采样过程中赋予经验回放中样本的优先级。
依据 TD 误差来为经验回放中的样本赋予不同优先级。TD 误差最开始我们是在时序差分方法的提到的,广义的定义是值函数(包括状态价值函数和动作价值函数)的估计值与实际值之差,在 DQN 算法中就是目标网络计算的 值和策略网络(当前网络)计算的 值之差,也就是 DQN 网络中损失函数的主要构成部分。
我们每次从经验回访中取出一个批量的样本,进而计算的 TD 误差一般是不同的,对于 DQN 网络反向传播的作用也是不同的。TD 误差越大,损失函数的值也越大,对于反向传播的作用也就越大。 这样一来如果 TD 误差较大的样本更容易被采到的话,那么我们的算法也会更加容易收敛。因此我们只需要设计一个经验回放,根据经验回放中的每个样本计算出的 TD 误差赋予对应的优先级,然后在采样的时候取出优先级较大的样本。
# C51 算法
分布式 DQN 算法,即 Distributed DQN,有时也会看到它也叫 Categorical DQN 这个名字,但最常见的名字是 C51 算法 。该算法跟 PER 算法一样,是从不同的角度改进强化学习算法,而不单单指 DQN 算法,而是能适用于任何基于 Q-learning 的强化学习算法。该算法的核心思想是将传统 DQN 算法中的值函数 换成了值分布 ,即将值函数的输出从一个数值变成了一个分布,这样就能更好地处理值函数估计不准确以及离散动作空间的问题。
在之前讲到的经典强化学习算法中我们优化的其实是值分布的均值,也就是 函数,但实际上由于状态转移的随机性、函数近似等原因,智能体与环境之间也存在着随机性,这也导致了最终累积的回报也会是一个随机变量,使用一个确定的均值会忽略整个分布所提供的信息。因此,我们可以将值函数 看成是一个随机变量,它的期望值就是 函数,而它的方差就是 函数的不确定性,公式表示如下:
其中状态分布